函数

函数的定义

x(自变量),f(法则),y(因变量)
x的范围称作定义域,y的范围称作值域

函数的基本性质

有界性
函数$f(x)$的定义域内,恒有$m≤f(x)≤M$,则称函数$f(x)$在该域内为有界函数
单调性
单调递增$f(x)$随着$x$的增加而增加
单调递减$f(x)$随着$x$的增加而减小
周期性
若$f(x) = f(x+t)$,则称$f(x)$为周期函数,$f(x)$的周期为t
常见:$f(x) = sinx,f(x) = cosx,$ T = 2$\pi$,$f(x) = |sinx|,f(x) = |cosx| ,f(x) = tanx$ T = $\pi$
奇偶性
定义:当函数$f(x)$的定义域关于原点对称时
奇函数:$f(-x) = -f(x)$,图形关于原点对称
偶函数:$f(-x) = f(x)$,圆形关于y轴对称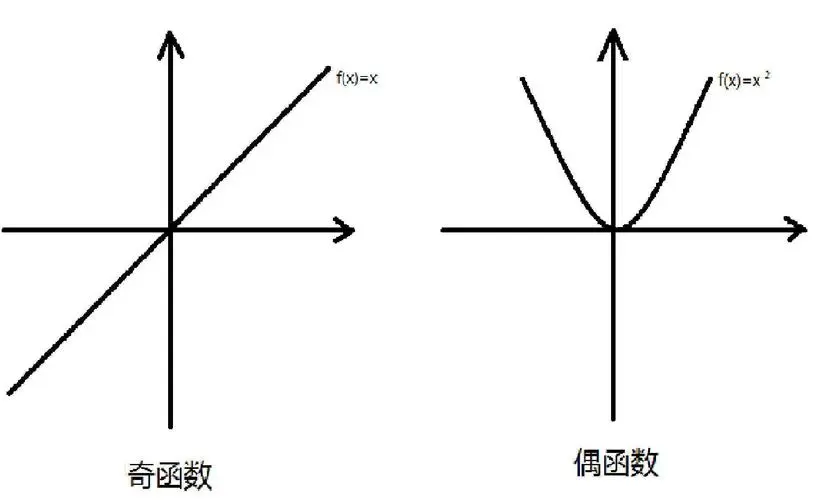

常见奇函数
-$sinx,arcsinx,tanx,cotx,x^{(奇数)}$
常见偶函数
-$cosx,|x|,x^{(偶数)}$
判断下列函数的奇偶性
例题:
例1: $f(x) = x^3+2x$
解

$f(-x)= -x^3 + -2x = -f(x) 函数为奇函数$

例2: $f(x) =xsinxe^{cosx}$
解

$f(-x) =-xsin(-x)e^{cos(-x)}$
$=-x(-sinx)·e^{cosx}$
$=x·sinx·e^{cosx} = f(x) 函数为偶函数$

例3: $f(x) = x(x^2-1)(x^3-1)$
解

$ f(-x) = -x[-(x^2)-1)][(-x)^3-1)]$
$ =-x(x^2-1)(-x^3-1)$
$ =-x(x^2-1)[-(x^3+1)]$
$ =x(x^2-1)(x^3+1) ≠f(x),-f(x) 函数为非奇非偶函数$

基本初等函数
幂函数 $y=x^a$(a为实数)
幂函数

1.$y=x,x,y \in R$ 奇函数
</div>
2.$y=x^{(-1)}=\frac{1}{x},x≠0,y \in R$ 奇函数
</div>
3.$y=x^2,x \in R,y>=0 偶函数$
</div>
4.$y=\frac{1}{2}=\sqrt{x},x,y>=0$
</div>
5.$y=x^3,x,y\in R$
</div>

四则运算
四则
1. $a^n·a^m \quad=\quad a{(n+m)}$
2. $a^n÷a^m \quad=\quad \frac{a^n}{a^m}$
3. $(a^n)^m \quad=\quad a^{(n·m)}$
4. $(\frac{b}{a}^n) \quad=\quad \frac{b^n}{a^n}$
5. $a^{(-n)} \quad=\quad \frac{1}{a^n}$
6. $a^{-\frac{1}{n}} \quad=\quad \sqrt[n]{a}$
三角函数
正弦 $y = sinx , x\in R,y\in[-1,1]奇函数$
余弦 $y = cosx , x\in R,y\in[-1,1]偶函数$
正切 $y = tanx = \frac{sinx}{cosx}$
三角函数等价关系
$y = sinx ⇆ y = cscx = \frac{1}{sinx}$
$y = cosx ⇆ y = secx = \frac{1}{cosx}$
$y = tanx = \frac{sinx}{cosx} ⇆ y = cotx = \frac{1}{tanx} = \frac{cosx}{sinx}$
三角函数基本公式
$1.sin^2a+cos^a = 1$ $2.tan^2a+1 = sec^2x$ $3.cot^2x+1=csc^2x$
二倍角公式
$sin2a = 2sina·cosa, cos^2x=cos^2x-sin^2x cos2a=1-sin^2x cos2a = 2cos^2x-1$
两角和与差
$sin(α+β) = sinαcosβ+cosαsinβ$ $sin(α-β) = sinαcosβ-cosαsinβ$
反三角函数
$D: -1≤x≤-1$ $1.y=sinx ⇆ y=arcsinx 2.y=cosx⇆y=arccosx 3. y=tanx⇆y=arctanx$
常函数
$y = C$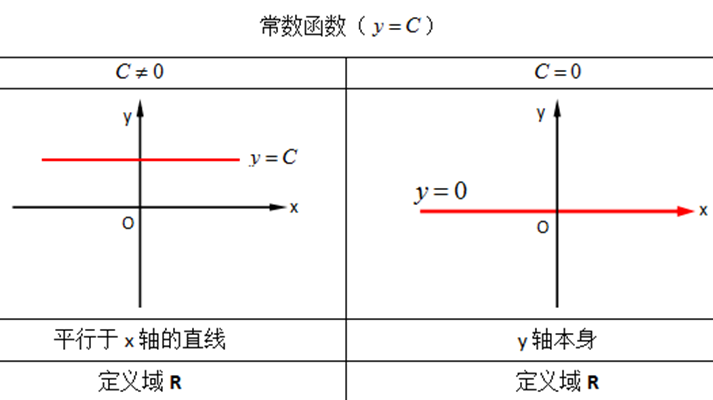

复合函数
定义:有多个函数复合组成
$y=f(u) , u=g(x) → y=f[g(x)] 例:y =ln(x+1),y=lnu,u=x+1$
基本初等函数
定义: 由基本初等函数与常数经过有限次的四则运算法则或符合构成
例: $y=sinx+x^2,y=ln(sinx),y=sinx+x^2+ln(xins)$
应用:求函数表达式
例1: $f(x+1) = x^2+2x,求f(x)$
解

$t=x+1,x=t-1,f(t)=(t-1)^2+2(t-1) = t^2-2t+1+2t-2=t^2-1,得出f(x)=x^1$

解

$f(x+1) = x^2+2x+1-1=(x+1)^2-1=f(x)=x^2-1$
函数定义域
$y = \frac{1}{x},x≠0|y=\sqrt[偶]{x},x≥0|y=\sqrt[奇]{x},x\in R$
$y=loga^x,y=lnx,x>0$
$y=arcsinx,arccosx,1≤x≤1$
$y =tanx, D:x≠k\pi+\frac{\pi}{2},k \in Z$
$y =cotx,D: x≠k\pi,k \in Z$
求函数定义域
例1. $y=ln(4-x^2)-\sqrt{x^2}{-1}$
解

$
\begin{cases}
& \text{} 4-x^2 \Rightarrow 4 >x^2 \Rightarrow -2<x<2 \\
& \text{} x^2-1 \Rightarrow x^2≥ 1 \Rightarrow x≥1,x≤1
\end{cases}
$

例2.$y=\frac{ln(x-1)}{\sqrt{2-x}}$

解

$
\begin{cases}
& \text{} \sqrt{2-x} ≠ 0 \Rightarrow 2-x ≠0 \Rightarrow x≠2 \\
& \text{} x-1>0 \Rightarrow x > 1
\end{cases}
$

抽象形函数

例1: 已知函数$f(x)$的定义域为(-1,1),求函数$f(2x-1)$的定义域
注:同一函数的括号的范围是相同的

解

$-1<x<1 \Rightarrow -1<()<1 \Rightarrow -1<2x-1<1 \Rightarrow 0<x<1$

例2:$f(1-3x)$的定义域为(-3,3],求$f(x)$的定义域

解

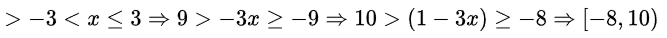
反函数

定义:反函数和原函数的x和y是相反的
$y=f(x),y=f^-1(x)$
$求反函数 1.x=y-1$ $2.x,y互换$
例1:求 $y=ln(x+1)的反函数$

解

$e=lnx=x,e^y=e^{ln(x+1)}=x+1$
$e^y=x+1,x=e^y-1 $

例2:求 $y=lnx+\sqrt{1+x^2}$ 的反函数

解

$e^y=e^{ln(x+\sqrt{1+x^2})}$
$e^y=x+\sqrt{1+x^2}$
$e^y-x=\sqrt{1+x^2}$
$(e^y-x)^2=1+x^2$
$e^{2y}-2xe^y+x^2=1+x^2$
$e^{2y}-2xe^y=1$
$e^{2y}-1=2xe^y$
$x=\frac{e^{2y}-1}{2e^x}$

函数

函数的定义

函数的基本性质

基本初等函数

四则运算

三角函数

三角函数等价关系

三角函数基本公式

二倍角公式

两角和与差

反三角函数

常函数

复合函数

基本初等函数

函数定义域

抽象形函数

反函数